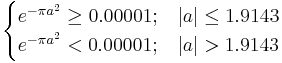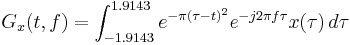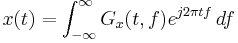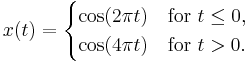Gabor transform

The Gabor transform, named after Dennis Gabor, is a special case of the short-time Fourier transform. It is used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time. The function to be transformed is first multiplied by a Gaussian function, which can be regarded as a window, and the resulting function is then transformed with a Fourier transform to derive the time-frequency analysis. The window function means that the signal near the time being analyzed will have higher weight. The Gabor transform of a signal x(t) is defined by this formula:

G_x(t,f) = \int_{-\infty}^\infty e^{-\pi(\tau-t)^2}e^{-j2\pi f\tau}x(\tau)\,d\tau

The Gaussian function has infinite range and it is impractical for implementation. But take a look at the distribution of Gaussian function.

\begin{cases} e^{-{\pi}a^2} \ge 0.00001; & \left| a \right| \le 1.9143 \\ e^{-{\pi}a^2} < 0.00001; & \left| a \right| > 1.9143 \end{cases}

Gaussian function with 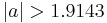\left| a \right| > 1.9143 can be regarded as 0 and also can be ignored. Thus the Gabor transform can be simplified as

G_x(t,f) = \int_{-1.9143}^{1.9143} e^{-\pi(\tau-t)^2} e^{-j2\pi f\tau} x(\tau) \, d\tau

This simplification makes the Gabor transform practical and realizable.

Contents

Inverse Gabor transform

The Gabor transform is invertible. The original signal can be recovered by the following equation

x(t) = \int_{-\infty}^\infty G_x(t,f) e^{j2\pi tf}\,df

Properties of the Gabor transform

The Gabor transform has many properties like those of the Fourier transform. These properties are listed in the following tables.

Signal Gabor transform Remarks
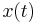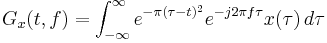x(t)\, G_x(t,f)=\int_{-\infty}^\infty e^{-\pi(\tau-t)^2}e^{-j2\pi f\tau}x(\tau)\,d\tau
1 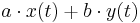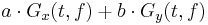a\cdot x(t) %2B b\cdot y(t)\, a\cdot G_x(t,f) %2B b\cdot G_y(t,f)\, Linearity property
2 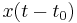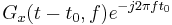x(t-t_0)\, G_x(t-t_0,f)e^{-j2\pi ft_0}\, Shifting property
3 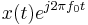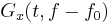x(t)e^{j2\pi f_0 t}\, G_x(t,f-f_0)\, Modulation property
Remarks
1 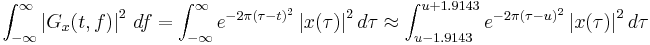\int_{-\infty}^\infty \left| G_x(t,f) \right|^2\,df = \int_{-\infty}^\infty e^{-2\pi (\tau-t)^2}\left| x(\tau) \right|^2 d\tau \approx \int_{u-1.9143}^{u%2B1.9143}e^{-2\pi (\tau-u)^2}\left| x(\tau) \right|^2 d\tau Power integration property
2 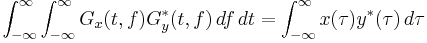\int_{-\infty}^\infty \int_{-\infty}^\infty G_x(t,f)G_y^*(t,f)\,df\,dt = \int_{-\infty}^\infty x(\tau)y^*(\tau)\, d\tau Energy sum property
3 \begin{cases} \displaystyle \int_{-\infty}^\infty \left| G_x(t,f) \right|^2df < e^{-2\pi(t-t_0)^2}\int_{-\infty}^\infty \left| G_x(t_0,f) \right|^2\,df; & \text{if } x(t) =0 \text{ for }t>t_0 \\[12pt] \displaystyle \int_{-\infty}^\infty \left| G_x(t,f) \right|^2\,dt < e^{-2\pi(f-f_0)^2}\int_{-\infty}^\infty \left| G_x(t,f_0) \right|^2\,dt; & \text{if } X(f) =FT[x(t)] = 0 \text{ for }f>f_0 \end{cases} Power decay property
4 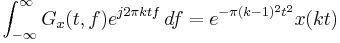\int_{-\infty}^\infty G_x(t,f) e^{j2\pi ktf}\,df = e^{-\pi (k-1)^2 t^2} x(kt) Integration property
5 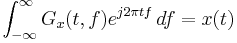\int_{-\infty}^\infty G_x(t,f) e^{j2\pi tf}\,df = x(t) Recovery property

Application and example

The main application of the Gabor transform is used in time frequency analysis. Take the following equation as an example. The input signal has 1Hz frequency component when t ≤ 0 and has 2Hz frequency component when t > 0

x(t) = \begin{cases} \cos(2\pi t) & \text{for } t \le 0, \\ \cos(4\pi t) & \text{for } t> 0. \end{cases}

But if the total bandwidth available is 5Hz, other frequency bands except x(t) are wasted. Through time frequency analysis by applying the Gabor transform, the available bandwidth can be known and those frequency bands can be used for other applications and bandwidth is saved. The right side picture show the input signal x(t) and the output of the Gabor transform. As our expectation, the frequency distribution can be separate as two parts. One is t ≤ 0 and the other is t > 0. The white part is the frequency band occupied by x(t) and the black part is not used.

See also

References